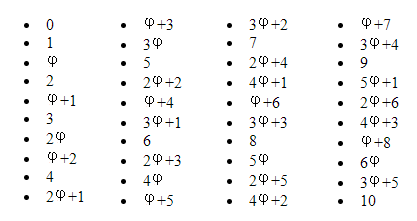Copyright©
2017-2021
www.ferroul.fr

Retour   

Question sur les longueurs des côtés des formes obtenues à l’aide de polyores

ou, plus mathématiquement parlant,

Conjecture sur les entiers de Dirichlet à coefficients positifs

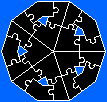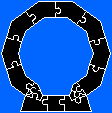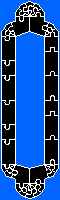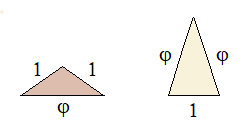
Les polyores sont des polymultiformes obtenues par juxtaposition des triangles d’or ci-dessous :

Les détails sur les polyores, sur La Ora Stelo, casse-tête dont les pièces sont des polyores, et sur le nombre d’or φ sont visibles ici.

Depuis peu, Kate Jones, qui commercialise La Ora Stelo, a rajouté, à ma demande, 3 pièces pour entourer (clôturer) les figures à réaliser avec les polyores.

Voici ces 3 pièces :

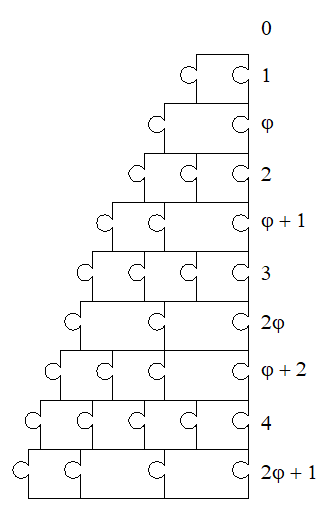
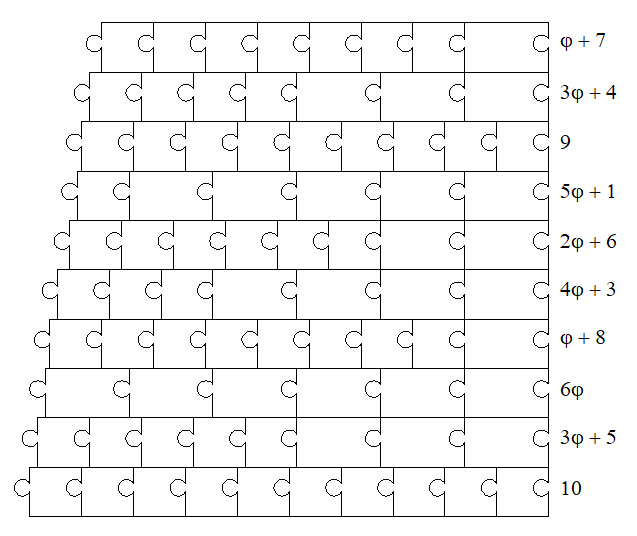
Ci-dessous les dimensions :

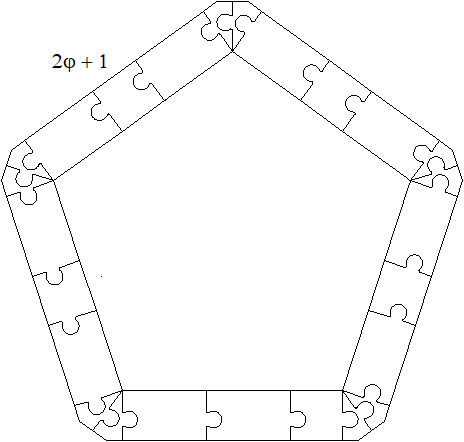
Voici un exemple de clôture pour un pentagone régulier dont les côtés mesurent 2φ + 1 :

Plus de détails sur les clôtures  ici.

Dans ses pages, Kate Jones donne les 148 plus petites valeurs possibles pour la longueur d’un côté d’une figure réalisée à l’aide de polyores.

Voici les 40 premières valeurs :

Les côtés des polyores et des formes obtenues à l’aide de polyores ont pour longueurs des nombres de la forme aφ + b où a et b sont des nombres entiers positifs.

Or les nombres de la forme mφ + n où m et n sont des nombres entiers relatifs sont appelés « entiers de Dirichlet » ; les longueurs des côtés des figures obtenues à l’aide de polyores sont donc des entiers de Dirichlet à coefficients positifs (dans la suite je les noterai entiers DCP).

Entre deux entiers de Dirichlet, il y a une infinité d’entiers de Dirichlet tandis qu’entre deux entiers DCP, il n’y a qu’un nombre fini d’entiers DCP. On peut, pour chacun de ces entiers, parler de l’entier suivant et, à part pour 0, de l’entier précédent.

Les valeurs données plus haut sont rangées par ordre croissant ; pour s’en faire une idée, voici la matérialisation de la première colonne à l’aide de bords droits :

et celle de la quatrième colonne :

Plus on augmente les dimensions, plus l’écart entre 2 valeurs successives diminue. Mais ce n’est que cette année que j’ai remarqué que cet écart est à chaque fois une puissance de φ à exposant négatif.

Ci-dessous, les 120 premiers entiers DCP par ordre croissant et, plus bas, les différences :

Ma conjecture : l’écart entre deux entiers de Dirichlet à coefficients positifs successifs est une puissance de φ à exposant négatif.

Question 1 : Est-ce que cette conjecture a déjà été formulée ?

Question 2 : Comment la démontrer ?

En attendant, on peut s’en servir pour trouver le suivant d’un entier DCP. Prenons par exemple 4φ + 7.

Ecrivons les puissances négatives de φ :

1, φ - 1, 2 - φ, 2φ – 3, 5 – 3φ, 5φ – 8, …

Les 5 premières peuvent être ajoutées à 4φ + 7 pour donner un autre entier DCP mais, avec 5φ – 8, on obtiendrait 9φ – 1 qui a un coefficient négatif.

5 – 3φ est la plus petite puissance de φ qu’on puisse ajouter à 4φ + 7 ; le résultat est φ + 12 : c’est l’entier de Dirichlet à coefficients positifs qui suit 4φ + 7.

Pour 30φ + 27, il faudra aller jusqu’à 34 - 21φ (celle d’après, 34φ - 55, ne convenant pas) et le suivant de 30φ + 27 est 9φ + 61.

Jacques FERROUL le 24/02/2021
jacques.ferroul[arobase]gmail.com