Copyright©
2017-2023
www.ferroul.fr

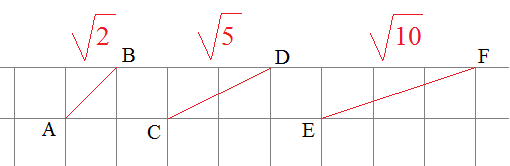
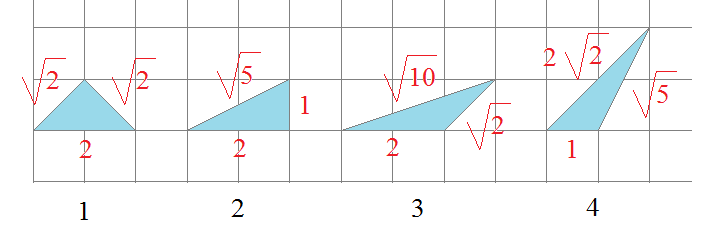
1) Introduction mathématique :

      Lorsque j’ai découvert, il y a fort longtemps, les pentominos, j’aimais chercher à reproduire chaque pentomino avec ses dimensions triplées.
Il fallait pour cela utilliser 9 pentominos (car 3² = 9).

      Avec les polytans (aussi appelés polyabolos par certains et polyisorthes par moi, j’en reparlerai plus tard) on pouvait multiplier les dimensions par √2 ou par 2√2.

      Avec les polyiapons, on peut multiplier les dimensions par √3 ou par 2√3.

      Avec les polyspidriapons, on peut aller jusqu’à 7√3 (voir Défis Polyspid’).

      J’ai voulu chercher un ensemble de racines carrées compatibles entre elles et j’ai choisi les racines carrées de 2, 5 et 10 car les multiples de ces racines auxquels on ajoute les nombres entiers, forment un ensemble stable pour la multiplication. De plus ces nombres sont les longueurs de segments joignant des intersections de lignes d’un quadrillage.

      Ci-dessus, les longueurs des segments [AB], [CD] et [EF] sont les racines de 2, 5 et 10 si on suppose que le côté des carrés du quadrillage mesure 1.

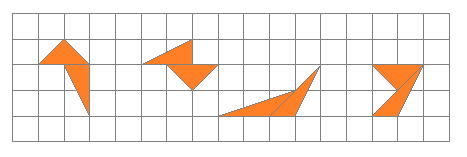
      Les triangles ci-dessous ont tous la même aire : c’est l’aire d’un carré du quadrillage.

      De plus leurs côtés ont des mesures qui sont des nombres entiers ou des multiples des racines de 2, 5 ou 10.

      Ils sont les triangles de base des polyrhizes qui sont donc obtenus par juxtaposition de triangles pris parmi ces 4.

2) Les polyrhizes :

      Les triangles bleus sont les 4 monorhizes ; les jaunes sont les 24 birhizes.

      Pour le moment il n’a pas de polyrhizes vendus ; vous pouvez les fabriquer vous-même mais ils ont cela d’intéressant que l’on peut résoudre les problèmes simplement avec un crayon sur du papier quadrillé.

3) Restrictions :

      a) Les associations suivantes n’ont pas été retenues car elles donnent des birhizes semblables aux birhizes 2, 3 et 12 :

      b) Les associations suivantes n’ont pas été retenues car un des sommets (marqué en rouge) n’est pas à une intersection de lignes du quadrillage :

      Les points d’intersection des lignes du quadrillage forment un réseau, aussi je dirais que les birhizes retenus sont « réseau-nables » et que les trois ci-dessus ne sont pas réseau-nables.

      c) Les associations suivantes n’ont pas été retenues car les juxtapositions se font par des côtés qui n’ont pas la même longueur ou qui sont décalés l’un par rapport à l’autre :

      Comme ce sont tout de même des figures réseau-nables, il n’est pas exclu qu’un jour je les étudie de plus près (à moins que vous ne vous en chargiez !).

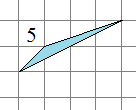
      d) J’ai longtemps travaillé sur les 4 monorhizes retenus mais dernièrement j’ai découvert un nouveau triangle qui pourrait convenir (il a une aire de 1) :

      Ce serait un cinquième monorhize qui amènerait des birhizes supplémentaires ; c’est aussi une piste à étudier.

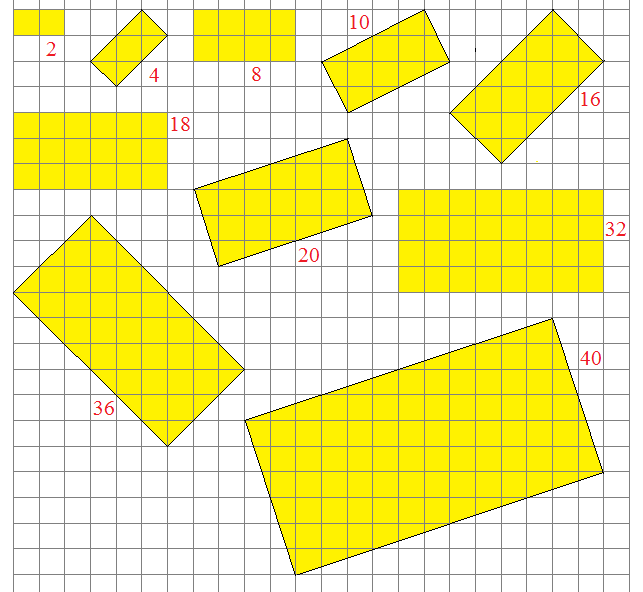
4) Formes à reconstituer : A l’aide de certains des 24 birhizes et éventuellement de certains des 4 monorhizes, essayez de reconstituer les rectangles suivants (les aires sont marquées en rouge):

      Par exemple, le rectangle d’aire 16 peut être reconstitué à l’aide de 8 birhizes.

      Le rectangle d’aire 20 peut être essayé avec 10 birhizes ou 9 birhizes et 2 monorhizes.

      Le rectangle d’aire 2 est le birhize 08.

---

      Vous pouvez aussi jouer avec des Polyrhizes sur votre ordinateur. Il y a :

      • 17 formes : Polyrhizes

      Allez sur Jeux de Tess pour des explications à propos de Ruffle, logiciel gratuit qui permet de faire fonctionner les jeux sur fichiers .swf de l’ancien Flash Player.

---

Jacques FERROUL le 21/10/2023
jacques.ferroul[arobase]gmail.com